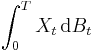Progressively measurable process

In mathematics, progressive measurability is a property in the theory of stochastic processes. A progressively measurable process, while defined quite technically, is important because it implies the stopped process is measurable. Being progressively measurable is a strictly stronger property than the notion of being an adapted process.^[1] Progressively measurable processes are important in the theory of Ito integrals.

Definition

Let

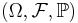$(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space;
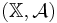$(\mathbb{X}, \mathcal{A})$ be a measurable space, the state space;
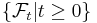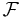$\{ \mathcal{F}_{t} | t \geq 0 \}$ be a filtration of the sigma algebra $\mathcal{F}$ ;
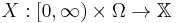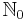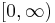$X�: [0, \infty) \times \Omega \to \mathbb{X}$ be a stochastic process (the index set could be $[0, T]$ or $\mathbb{N}_{0}$ instead of $[0, \infty)$ ).

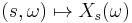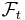The process $X$ is said to be progressively measurable^[2] (or simply progressive) if, for every time $t$ , the map $[0, t] \times \Omega \to \mathbb{X}$ defined by $(s, \omega) \mapsto X_{s} (\omega)$ is $\mathrm{Borel}([0, t]) \otimes \mathcal{F}_{t}$ -measurable. This implies that $X$ is $\mathcal{F}_{t}$ -adapted.^[1]

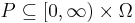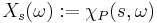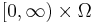A subset $P \subseteq [0, \infty) \times \Omega$ is said to be progressively measurable if the process $X_{s} (\omega)�:= \chi_{P} (s, \omega)$ is progressively measurable in the sense defined above. The set of all such subsets $P$ form a sigma algebra on $[0, \infty) \times \Omega$ , denoted by 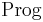$\mathrm{Prog}$ , and a process $X$ is progressively measurable in the sense of the previous paragraph if, and only if, it is 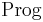$\mathrm{Prog}$ -measurable.

Properties

It can be shown that 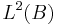$L^2 (B)$ , the space of stochastic processes $X�: [0, T] \times \Omega \to \mathbb{R}^n$ for which the Ito integral

$\int_0^T X_t \, \mathrm{d} B_t$

with respect to Brownian motion $B$ is defined, is the set of equivalence classes of 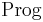$\mathrm{Prog}$ -measurable processes in $L^2 ([0, T] \times \Omega; \mathbb{R}^n)\,$ .

Every adapted process with left- or right-continuous paths is progressively measurable. Consequently, every adapted process with càdlàg paths is progressively measurable.^[1]
Every measurable and adapted process has a progressively measurable modification.^[1]

References

^ ^a ^b ^c ^d Karatzas, Ioannis; Shreve, Steven (1991). Brownian Motion and Stochastic Calculus (2nd ed.). Springer. pp. 4–5. ISBN 0-387-97655-8.
^ Pascucci, Andrea (2011) PDE and Martingale Methods in Option Pricing. Berlin: Springer

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›